Diving Deep Into Quantum Computing: Modern Cryptography
By Morton Swimmer, Mark Chimley, Adam Tuaima
 Cryptography is at the core of computer security. And while we often take cryptography for granted, new technological developments are posing a threat to our current cryptographic approaches. For now, core cryptographic algorithms can withstand evolving attacks. But this could change with quantum computing, which will have practical applications in the next five to ten years. Quantum computing is a computing technology that uses the laws of quantum mechanics to solve complex problems far better and faster than classical computers. This is why it is a good idea for companies to devote attention to post-quantum cryptography now and plan for cryptographic migration well in advance.
Cryptography is at the core of computer security. And while we often take cryptography for granted, new technological developments are posing a threat to our current cryptographic approaches. For now, core cryptographic algorithms can withstand evolving attacks. But this could change with quantum computing, which will have practical applications in the next five to ten years. Quantum computing is a computing technology that uses the laws of quantum mechanics to solve complex problems far better and faster than classical computers. This is why it is a good idea for companies to devote attention to post-quantum cryptography now and plan for cryptographic migration well in advance.
The threat of quantum computers is real: threat actors may already be hoarding our network traffic today so they can decrypt it when quantum computing finally enables them to do so. This is called a harvest attack. Thus, moving to post-quantum cryptography may soon be in a company’s best interest — especially since companies are left with just a short timeframe to develop and implement a plan.
This is the first installment of a four-part series on post-quantum cryptography. Here we will start our series by discussing contemporary cryptography and its branches: symmetric and asymmetric cryptography. We also tackle what defenders need to be aware of when it comes to developing a quantum-resistant cryptography plan.
Symmetric encryption
A common key
The basic concept of symmetric cryptography is that the same key is held by both the encrypting and decrypting users. We'll use a padlock analogy to explain the fundamental concepts behind cryptographic techniques. Figure 1 shows an analogy for symmetric cryptography.
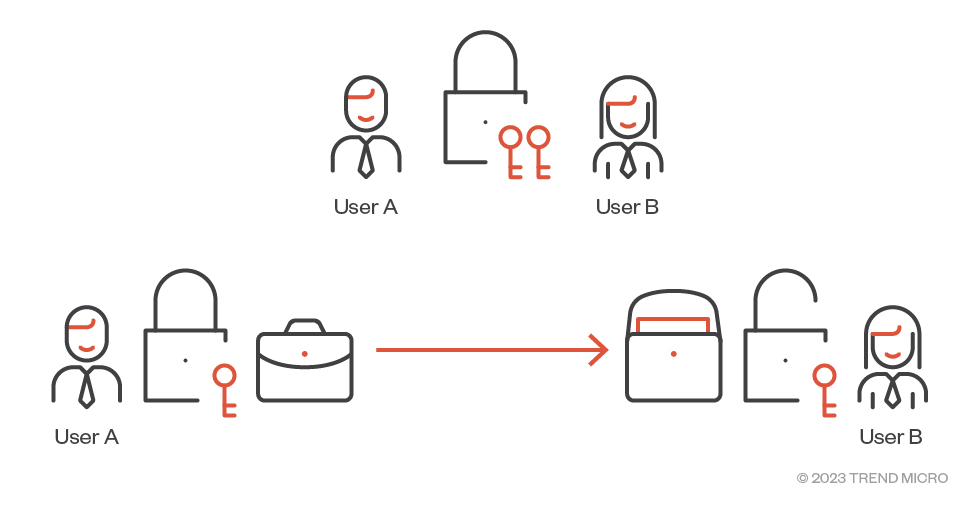
Figure 1. In the symmetric cryptography analogy, both User A and User B (the encrypting and decrypting users) hold identical keys to the same padlock.
User A wishes to send a document securely to User B so that nobody else can see it while it is in transit. Before this can occur, both users get together and buy a padlock which comes with two identical copies of the key. They each take a key. When either user wishes to send the document, they place it in a briefcase which they lock with the padlock. The locked briefcase can now be securely sent and the other user can unlock it to retrieve the document.
A locked briefcase is just an analogy, so we’ll take a look at how symmetric encryption algorithms are actually constructed to protect digital information. To help distinguish between symmetric and asymmetric encryption, we’ll also use the notation “symmetric cipher” in place of “symmetric encryption.”
One-time pad
The simplest — and most secure — type of encryption is a one-time pad.

Figure 2. An example of a one-time pad
The idea is that the plain-text (shown in Figure 2 as a stream of bits at the top) is exclusively OR'd with a key stream (middle) to produce the cipher-text at the bottom. The key stream is shared by the sender and receiver. To decrypt it, one would simply need to XOR the cipher-text with the same keystream.
A one-time pad is a completely secure method of encryption, but it has some major drawbacks:
- The keystream must be exactly the same size as the message to be encrypted.
- The same keystream must be used for encryption and decryption.
- The keystream must only be used once for any particular message.
These factors limit the usefulness of the one-time pad, but it is an important concept to bear in mind, especially since many symmetric ciphers are built upon this basic idea. In particular, if a keystream could be generated by a function, which is initiated by a key, then only this key would need to be shared between the encrypting and decrypting parties rather than the whole key stream. This is exactly what symmetric encryption algorithms do.
A basic symmetric cipher
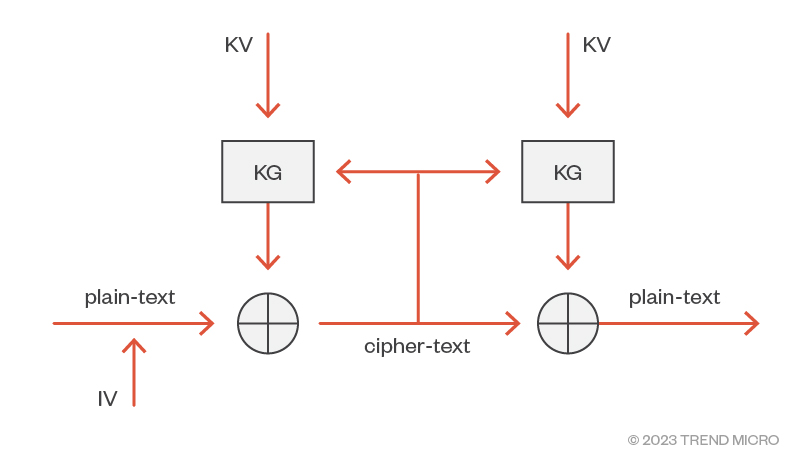
Figure 3. Construction of a symmetric cipher
Figure 3 shows how a symmetric cipher can be constructed. The function that generates the key stream is known as the key-(stream) generator (KG). The common keys shared by the encryptor and decryptor are known as key variables (KV).
The rest of the structure is the same as that of the one-time pad: the plain-text is exclusively OR'd with the key-stream output from the encrypting KG, and it’s decrypted by XOR'ing with the key-stream output from the decrypting KG.
The only additional item in the diagram is the presence of an initialization vector (IV). This is a random-but-not-secret value that is appended to the start of the plain-text. Its purpose is to ensure that two identical plain-text messages get encrypted to different cipher-text outputs. How this can be done is dependent on the mode in which the algorithm operates and is the subject of a later section.
Stream and block ciphers
The simple cipher function described in the previous section is an example of a stream cipher because it operates on a stream of bits. The development of cryptography stems largely from military applications where the protection of communications was the primary requirement. Because of this legacy, stream ciphers were the first algorithms to be developed.
For wider use of cryptography (and certainly, in commercial environments), the protection of a communication stream is not relevant, and a more general concept of encrypting a block of data is more appropriate. Most modern symmetric algorithms are, therefore, block ciphers. These operate on blocks of data rather than a stream of bits. The Advanced Encryption Standard (AES), for example, has a block size of 128 bits. AES produces 128 bits of output at a time, which is then combined with the plain-text in some way (depending on the mode) to produce the cipher-text.
Asymmetric cryptography
Public and private keys
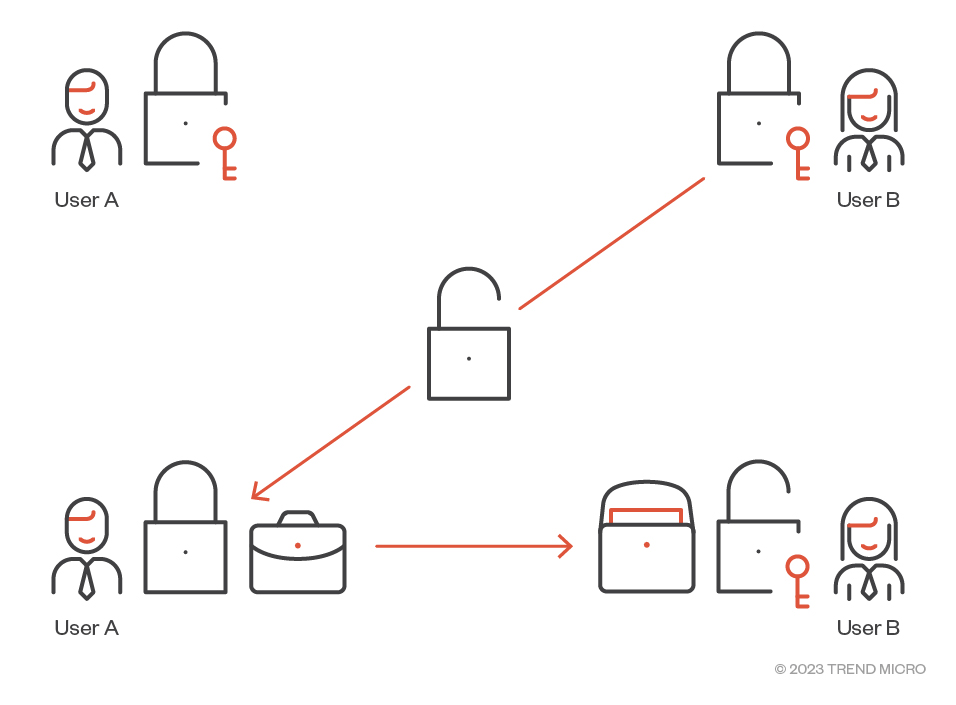
Figure 4. In the asymmetric cryptography analogy, Users A and B each have their own keys to their own padlocks.
Returning to the analogy of sending a document inside a locked briefcase, the concept of asymmetric cryptography or public key cryptography (PKC) is shown in Figure 4. The two parties, A and B, each buy their own padlocks and thus have different keys. A crucial difference to the symmetric case is that A and B don't have to meet up to share a copy of the same secret key. Instead, B opens her padlock and sends it (opened) to A. As before, A puts the document in the briefcase, locks it with B's padlock and sends the locked briefcase to B. Now the only person who can open the briefcase is B.
Similarly, A could unlock his padlock and send it to B. Then, B can lock the briefcase with A’s padlock and return the secured briefcase to him. In this analogy, the opened padlocks are public keys (in a cryptographic sense) and the padlocks' keys are private keys.
The features of asymmetric cryptography
The attribute of asymmetric techniques that makes them asymmetrical is that different keys are used for encryption and decryption. Typically, each user will have a pair of keys, one of which is public, while the other is private. For encryption, the recipient's public key is used and for decryption, the recipient uses their private key. The primary benefit of asymmetric techniques over symmetric ciphers is that the two parties do not need to pre-share any secret information.
Asymmetric techniques tend to be based around an underlying “primitive hard problem”. The hard problem (which is referred to as a “primitive” for brevity) is usually a mathematical operation that is very time-intensive to compute. Common examples are the factorization of large composite numbers or computing logarithms in a finite group.
Digital signatures
In addition to the elimination of secret key-sharing for encryption, asymmetric techniques can also provide other useful functions, one of which is a digital signature. A digital signature is a logical equivalent of someone's physical signature on a piece of paper; it provides assurance that the document upon which it resides genuinely originated from the signer. To translate this idea into logical terms, a digital signature is a value that depends on two things: the information being signed, and a secret known only to the signer.
Digital signatures are probably the most widely used form of asymmetric cryptography since they are used anywhere where authenticity is required, such as verification of a piece of software or a financial transaction.
Cryptographic systems
A cryptographic system (cryptosystem) is a coherent set of cryptographic services, functions, and algorithms that address a set of security problems within a defined domain. Though this is a fairly loose definition, the key point is that a cryptosystem is designed with a security problem in mind and it is designed to achieve protection against that problem within the bounds of the system. Therefore, a cryptosystem must have been analyzed and shown to be effective within its scope.
The following sections describe some of the design features that are used to form cryptosystems.
Symmetric cipher modes
Recall that the first symmetric ciphers were stream ciphers used to protect communications. Communication channels are prone to data errors. So, if an error occurs during the transmission of cipher-text, it could be disastrous because the resulting keystream might be out of sync with the data, resulting in a nonsensical, plain-text output. To counter this problem, stream ciphers are often implemented with a form of feedback whereby the output of the KG or the encryption is used in the formation of the next bit of the keystream. This gives the stream cipher a self-synchronizing capability, so that if sections of cipher-text are lost, the decryption eventually recovers to reveal the correct plain-text.
Similar feedback mechanisms can also be applied to block ciphers. The general idea of operating a cipher in a certain logical construction is known as a “mode of operation.” The most basic mode for a block cipher is an electronic codebook (ECB). Here, there’s no feedback and each block of output from the algorithm is XOR'd with a block of plain-text in sequence. While simple, ECB has some nasty drawbacks, one of which can plainly be seen in Figure 5.

Figure 5. An example of the result of a block cipher after it is operated in ECB
Source: Larry Ewing
Other modes of operation (which are more secure than ECB) include cipher feedback (CFB), output feedback (OFB), cipher-block chaining (CBC), counter (CTR), Galois/Counter mode (GCM) and XEX-based tweaked-codebook cipher-text stealing (XTS) mode. Most of these modes require the use of an IV and many will extend the size of the cipher-text compared with the plain-text, usually up to a multiple of the block size.
Data integrity
When considering the need for cryptography, it is easy to fall into the trap of just considering confidentiality or keeping information secret. Encryption algorithms enable you to do this, but often, confidentiality is not a sufficient attribute to make a system secure.
As an example, consider making an electronic bank transaction and requesting payment of a sum of money from your account to someone else. With an encryption algorithm such as AES, we can encrypt the request: “Pay the sum 12345 to recipient abcde.”
An attacker intercepting the encrypted transaction will only see something like: “hahehdhE438hdadjh9dh289daH8Hh823A”.
If, for instance, the attacker was able to modify some of the cipher-text, they might change just one or two bytes: “hahehdhE438hefdjh9dh289daH8Hh823A”.
If they were lucky (or quite ingenious) they might find that the decrypted transaction has become: “Pay the sum 95345 to recipient abcde.”
This would appear to be a genuine request which the bank would then process. It should be clear to the reader that in this example, encryption alone has not provided a sufficiently secure system for electronic banking.
One way such an attack could be prevented is to use a message authentication code (MAC) in addition to the encryption. A MAC is basically a keyed hash function; it requires a secret key and when it’s applied to a piece of data, it gives a cryptographic check to ensure that the data hasn’t been modified prior to being decrypted.
Authentication
In many applications, it is important to know the origin of a piece of information to be able to verify that it is genuine. The most common example is certificates that are used to send encrypted information to a website. What is a certificate? Earlier we discussed what digital signatures are, and a certificate is simply a signed public key. So, when you start an encrypted web session (possibly using TLS) with your favorite online shopping service provider, the service provider will need to send you their public key so that you can encrypt your credit card details and other credentials in such a way that only they can decrypt it. But how do you know the service provider’s website hasn’t been hacked and that there isn’t a man-in-the-middle sending you a falsified public key?
Instead of just sending you a public key, the service provider will send a signed public key, or a public key that’s been signed by a trusted third-party. Assuming you have the public key of the trusted third-party, you can then verify the signature of the certificate and trust the public key of your chosen service provider. Obviously, this chain of certificates has a limit: there are usually only three layers of hierarchy in commonly used X.509 certificates that protect website traffic.
Hybrid systems
Earlier, we discussed symmetric and asymmetric cryptographic techniques. Symmetric algorithms tend to be based on logical operations such as XOR or AND, whereas asymmetric techniques usually rely on mathematical operations such as exponentiation or multiplication. Asymmetric methods are only secure if the size of the elements or numbers in the operations are very big, typically greater than 1,024 bits and often much more so.
Computers are very efficient at performing logical operations, but even with fast multi-precision arithmetic, the mathematical operations required for asymmetric cryptography are significantly slower. Asymmetric techniques have the added drawback of only being applied to data of a constrained size at times.
These two limitations of asymmetric cryptography can be mitigated using a compromise whereby a system uses an asymmetric method to transmit or exchange a symmetric key. The symmetric key is then used to encrypt the data. Such a system is called a hybrid system. Hybrid systems are widespread, TLS (the successor of SSL) and key encapsulation mechanism (KEM)/data encryption mechanism (DEM) being two examples.
Key management
Having decided on our problem domain, chosen an appropriate algorithm or a set of them, and conducted a security analysis to validate the security of our solution, can we safely assume the work of designing a cryptosystem is done? Unfortunately, the answer is no. There is a very important piece we have yet to consider: how are all the keys going to be handled? Even if we assume that we’ll use a hybrid system so that users generate their own public/private key pairs, we would then need to ensure that we can verify the authenticity of shared public keys. We can do that using certificates, but then we would need to find a way to handle the hierarchy of certificates and share them among all users of the system.
The previous paragraph shows how the concept of a public key infrastructure (PKI) grew. PKI-based systems need careful planning and management, otherwise, they can quickly spiral out of control and lead to dangerously insecure practices. Arguably, one such example is perhaps X.509 certificates, which are used to protect nearly all secure web traffic. There are now so many untrusted certificates, certificates with different levels of trust, and different ways of locally managing certificate and revocation lists, that this particular PKI system is considered by some as being distinctly broken.
Regardless of the cryptographic algorithm or system being used, managing keys is an essential and, oftentimes, a more difficult task than determining how to encrypt data.
Attacks against cryptography
In the previous sections, we have described how cryptography, in practice, is a far more complex matter than simply employing one or another encryption algorithm. Weaknesses in cryptographic systems tend to occur through errors in the design of cryptosystems, their key management processes, or poor practices in implementing algorithms in software. The underlying cryptographic algorithms that we use today are generally impervious to direct attacks upon them, so attackers will almost always look for ways to exploit a potential weakness in the implementation or the design of the system as a whole.
The advent of quantum computing has disrupted the above principle of broadly universal trust in our underlying cryptographic algorithms. Consequently, we now need to start thinking about prospects, in the perhaps not-so-distant future, where our current suite of algorithms can be broken. We need to start thinking about that now because, in many cases, the information that we encrypt today needs to stay securely encrypted for a number of years into the future. Before considering how quantum computers can attack today’s cryptographic algorithms, we first need to look at the best methods of attack using classical computing.
The most common cryptographic algorithms In use today are considered safe from attacks because the best-known algorithms for attacking them are infeasible to implement or run at the required key sizes. As discussed above, common cryptographic algorithms – used for internet security, in phones, and for financial transactions – employ a few fundamental primitive mathematical operations which they rely on for their security. Encryption of data is almost always performed using a symmetric algorithm, which will most likely be AES. A symmetric algorithm’s keys are shared, agreed-on, or encapsulated using an asymmetric algorithm of various kinds. Beneath nearly all asymmetric algorithms are either of two fundamental mathematical security primitives: factorization and discrete logarithms.
Cryptographic primitives
Since learning our multiplication tables at school, we know that 15 = 3 x 5, but most people don’t know what the prime factors of 2023 are. With some work, we can see that 2,023 = 7 x 172. To do so, we use the simplest technique: trial division of prime numbers up to the square root using pencil and paper. The number 2,023 has a binary representation of 11111100111 so it takes 11 bits in a computer to represent it. Lengthening a number by one bit amounts to multiplying it by two, so we don’t have to lengthen an 11-bit number space very much before trial division (especially on paper) becomes infeasible for numbers of that size.
A logarithm is a function which finds exponents. When representing 2,023 in binary in a computer, we need to know how much space it needs. What we’re calculating is a value x for which 2,023 = 2x. The log2 function does this: x = log2(2x) and log2(2,023) = 10.982280605 hence 2,023 needs 11 bits to store it in a computer.
The cryptographic primitive of a discrete logarithm is similar to this, but the numbers we’re using are constrained to stay within a confined range: 0 - n-1. Sets of numbers like this with suitably defined mathematical operations such as addition or multiplication are known as finite groups. Arithmetic operations in finite groups give results that stay within the group. Just like a clock where seven hours after 11 p.m. is 6 a.m., the numbers in a finite group simply wrap round. Thus, a discrete logarithm amounts to finding x from a number y = gx 'modulo n', i.e., y = g times g (wrapped modulo n) times g (wrapped modulo n), repeated x times.
Solving the primitives
For asymmetric cryptographic algorithms, there is one leading general-purpose algorithm which can ostensibly solve the mathematical security primitives underlying them all: the general number field sieve (GNFS). It’s only worth looking at algorithms that can solve primitives where the numbers and the groups they reside in are of a general type. Various cryptographic algorithms have been devised, which rely on some special property of the system (usually, its group of numbers), but history has shown that special attacks often emerge against these special properties. Consequently, it’s a good rule of thumb to ensure that your cryptosystem only relies on mathematical security primitives for general numbers.
The number field sieve (NFS) was originally developed from methods for solving discrete logarithms, but it was soon adapted to solve factorizations. The improved versions of the NFS for factorization were then applied to its discrete logarithm version, too. The algorithm’s development is described in a paper by Carl Pomerance. Since the NFS has versions that work against the two fundamental primitives beneath nearly all asymmetric algorithms in use today, its successes provide a useful guide to the state of the art for attacking asymmetric cryptography in general.
Another point worth making is that many contemporary cryptographic systems use elliptic curve versions of the discrete logarithm primitive. Elliptic curves are used because they provide more efficient algorithms for a given level of security than algorithms employed over finite groups of integers. The discrete logarithm problem (DLP) has an analog within elliptic curve groups (of points on the curves) called the elliptic curve discrete logarithm problem (ECDLP). While there are some algorithms that work directly against the ECDLP primitive, there is a simple translation, known as MOV, which converts ECDLP to DLP, and thus allows the NFS to be used. Direct attacks against ECDLP are not orders of magnitude faster than MOV + NFS. So, for the purposes of this analysis, we can just look at NFS as the de facto benchmark of attacks against asymmetric algorithms.
The graph in Figure 6 shows the progression of factorization records for general integers. Not all the records will have been achieved using the NFS, but the latest ones certainly will. What’s noticeable from the graph (the data for which was obtained from Wikipedia) is that it's essentially linear in date versus bit-length, so it's taken about 25 years to double the capability of the attacks from about 400 to about 800 bits.
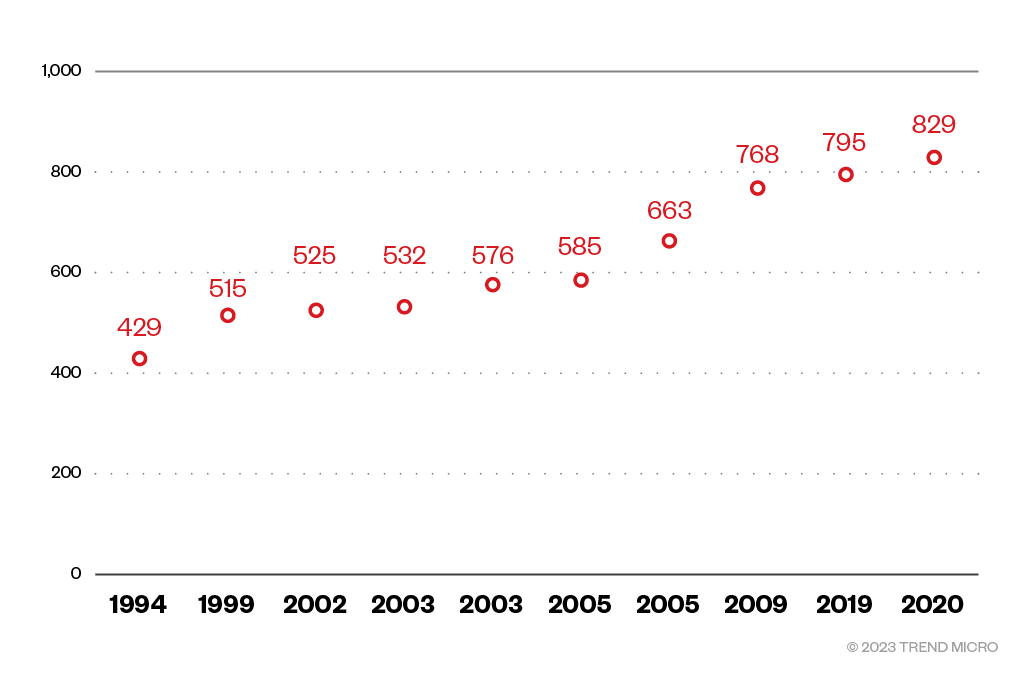
Figure 6. General integer factorization records
Discussion of the feasibility of using the NFS to attack asymmetric cryptography needs to consider the complexity of the algorithm. A discussion of algorithmic complexity will require a whole section in itself, so it will suffice to state that the NFS has a “sub-exponential” running time of about 2O(³√n). This means that adding one extra bit to the length of an asymmetric key (thus doubling the size of that key as a number) results in more than double the running time of the NFS. What the graph does not show is the running time of the algorithms used in the factorization records, nor does it show how much energy was used in the computations. However, based on some simple extrapolations, it certainly looks like 2,000-bit numbers will be safe from factorization by the NFS for at least 40 years.
What about symmetric algorithms? There is no underlying number theoretic mathematical primitive within algorithms such as AES. Instead, symmetric ciphers tend to be based on iterative functions in linear algebra. Attacking these ciphers amounts to unwinding the interactions within the algorithm to then express the cipher as a set of linear equations. In “Essential Algebraic Structure within AES,” Sean Murphy concludes that “...the security of the AES is equivalent to the solubility of certain extremely sparse multivariate quadratic systems over GF(28).” To date, the best-known direct attack against the AES cipher is not much better than a brute-force search of the keyspace.
Conclusion
In this article, we have presented an introduction to contemporary cryptography, explaining how there are two essential branches: symmetric and asymmetric. We described how the basic algorithms in each branch are constructed and how these algorithms are used to form complete cryptosystems. We gave brief descriptions of some of the considerations that need to be given when designing and implementing cryptosystems. It is within this area that vulnerabilities in cryptography tend to occur rather than in core algorithms themselves.
Finally, we examined how well core algorithms have stood up to improvements in direct attacks against them. The mathematical and cryptanalytic techniques of attacking core algorithms have improved at a roughly linear pace in relation to cryptographic key bit size. This means it has been relatively easy to future-proof cryptography by simply ensuring that the key size is sufficiently large enough to provide a requisite number of years’ protection for data.
As we will see in succeeding articles in this series, the emergence of quantum computing presents a challenge to the stable state of contemporary cryptography. Steady, incremental increases in key size may soon be insufficient to provide protection for core cryptographic algorithms against attacks by quantum computers.
Like it? Add this infographic to your site:
1. Click on the box below. 2. Press Ctrl+A to select all. 3. Press Ctrl+C to copy. 4. Paste the code into your page (Ctrl+V).
Image will appear the same size as you see above.
Recent Posts
- Cracking the Isolation: Novel Docker Desktop VM Escape Techniques Under WSL2
- Azure Control Plane Threat Detection With TrendAI Vision One™
- Forecasting Future Outbreaks: A Behavioral and Predictive Approach to Proactive Cyber Risk Management
- Fault Lines in the AI Ecosystem: TrendAI™ State of AI Security Report
- The Industrialization of Botnets: Automation and Scale as a New Threat Infrastructure

 Fault Lines in the AI Ecosystem: TrendAI™ State of AI Security Report
Fault Lines in the AI Ecosystem: TrendAI™ State of AI Security Report Cracking the Isolation: Novel Docker Desktop VM Escape Techniques Under WSL2
Cracking the Isolation: Novel Docker Desktop VM Escape Techniques Under WSL2 The AI-fication of Cyberthreats: Trend Micro Security Predictions for 2026
The AI-fication of Cyberthreats: Trend Micro Security Predictions for 2026 Stay Ahead of AI Threats: Secure LLM Applications With Trend Vision One
Stay Ahead of AI Threats: Secure LLM Applications With Trend Vision One